A koncepció a folytonosság

Definíció. f (x) függvény. meghatározott szomszédságában a. és ez az úgynevezett folyamatos a ponton. ha (1)

Így, az f függvény folytonos egy. ha az alábbi feltételek teljesülnek:

1. Az f függvény a szomszédságában a. azaz van egy szám, amely az U;

Meghatározása folytonossági f (x) egy. által kifejezett feltétel (1) lehet kiszerelni a segítségével (a nyelv), és használata környéke szempontjából szekvenciák rendre mint

Kiemeljük, hogy a meghatározás a folyamatosság, ellentétben a meghatározása a határérték akkor tekinthető befejezettnek, és nem szúrjuk szomszédságában egy pontot. és a határ a függvény értéke a függvény a pont.

Hívjuk x a különbség - a növekmény az érvelés és legyen x. és a különbség az f (x) - f (a) - a növekmény funkciót. megfelel egy adott növekmény az érvelés x. és hagyja, hogy y. Így

X = X - egy, y = f (x) - f (a) = f (a + x) - f (a).

Ezzel a jelöléssel (1) egyenlet formájában

Így, a folytonosság a pont azt jelenti, hogy egy végtelenül növekmény az érvelés megfelel egy infinitezimális növekmény funkciót.

Ennek analógiájára a koncepció a határ a bal (jobb) bevezette a folytonosság a bal (jobb). Ha az f függvény az intervallumon és. t.e.f (a - 0) = f (a). akkor ez a funkció az úgynevezett bal folytonos a.

Hasonlóképpen, ha a f függvény intervallumon, és f (a + 0) = f (a). akkor ez a funkció az úgynevezett jobbról folytonos egy.

Például, az f (x) = [x] folytonos jogot az x = 1, és nem folyamatos a bal oldali ezen a ponton, mivel f (1 - 0) = 0, F (1 + 0) = f (1) = 1.

Nyilvánvaló, hogy a függvény folytonos ezen a ponton, ha és csak akkor, ha a folyamatos, mind a jobb és a bal ezen a ponton.

A 2. lépésben azt feltételezzük, hogy a függvény a szomszédságában egy kilyukadt.

Egy pont az úgynevezett egy töréspontot egy f függvény. Ha ezt a funkciót vagy nem definiált egy, vagy meghatározott, de nem folyamatos egy.

Következésképpen, és - egy pont a diszkontinuitás f. ha nem végzik el legalább az alábbi feltételeknek:

2) van egy véges

Ha egy - egy f töréspontot, és ezen a ponton vannak véges határok a bal és a jobb, vagyis a lényeg az úgynevezett elsőrendű töréspontot.

Egyoldalú folytonosság. Besorolás pontok abbahagyni.

5.4.1. Meghatározása kétoldalas folytonosságot.

Annak megállapítására, a folytonosság a függvény x0 meglétét és az egyenlőséget. Az alkalmazás az egyoldalú határértékeket fogalom határozza meg a folytonosság a funkciót a bal és a jobb:

Opr.5.1.7. f (x) függvény folytonos egy ponton x0 a bal oldalon, ha.

Opr.5.1.8. f (x) függvény folytonos x0 jobb, ha.

A f (x) az úgynevezett folyamatos intervallumon [a. b], ha ez a folyamatos intervallumban (a. b), folyamatos a jobb és bal folyamatos ponton b.

Megjegyzés. A függvény folytonos az [a, b] lehetnek nem folytonosak a A és B pontok (ábra. 1)

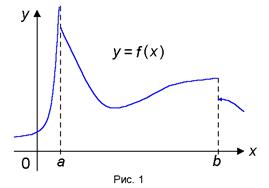
A beállított funkciók, amelyek folyamatos intervallumban [a. b] jelöli a C [a. b].

Tulajdonságok funkciók folyamatos intervallumon

Tétel 1 (v korlátozott folytonos függvény). Ha az f (x) folytonos intervallumon [a. b], arra korlátozódik, hogy ezt az intervallumot, azaz létezik egy számot C> 0, hogy „X Î [A. b] az | f (x) | ≤ C.

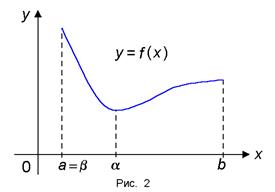
2. Tétel (Weierstrass). Ha az f (x) folytonos intervallumon [a. b], majd eléri a szegmensben a maximális érték M és minimális értéket m. azaz vannak olyan pontok # 945;. # 946; Î [A. b] úgy, hogy m = f (# 945;) ≤ f (x) ≤ f (# 946;) = M minden x Î [A. b] (2. ábra).

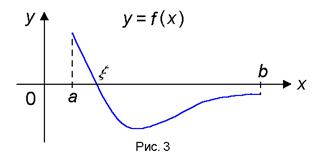
3. Tétel (létezését nulla). Ha az f (x) folytonos intervallumon [a. b] és a végpontokban veszi nulla értékek a különböző jelek, akkor az intervallum (. a b) létezik legalább egy ponton # 958; ahol f (# 958) = 0.

A geometriai jelentése a tétel, hogy a grafikon kielégíti a feltételeket, a tétel, biztos, hogy átlépje a OX tengely (3. ábra).

Megjegyzés. Ezen tétel alapú módszer közelítő egyenlet megoldása