monoton függvények

Meghatározása növekvő és csökkenő függvény

Let \ (y = f \ left (x \ right) \) egy differenciálható függvény az intervallum \ (\ left (\ right). \) Függvény növelésével (vagy nem csökkenő) egy adott időtartam, ha bármely pont \ (\ a \ left (\ jobbra), \) úgy, hogy \ (0, \) úgy, hogy \ [\ forall \ x \ in \ left (- \ delta,> \ right) \ Rightarrow f \ left (x \ jobbra) f \ left (> \ jobbra). \] hasonló módon határozzuk meg szigorúan csökkenő függvény \ (y = f \ left (x \ right) \) pontnál \ (. \)

A kritérium növekvő és csökkenő függvény

Tekintsük ismét a funkció \ (y = f \ left (x \ right), \) feltételezve a differenciálható egy intervallum \ (\ left (\ jobbra). \) Növekedése vagy csökkenése a funkciót a időközt az határozza meg a jel az első differenciálhányados.

1. Tétel.
Ahhoz, hogy működjön \ (y = f \ left (x \ right) \) nőtt az intervallumban \ (\ left (\ jobbra), \) szükséges és elégséges, hogy az első függvény deriváltját volt egy nem-negatív mindenütt ezen a tartományon belül: \ [f „\ left (x \ right) \ ge 0 \; \ forall \ x \ in \ left (\ right) \.] Ugyanez kritérium érvényes a funkció esetén, csökken az intervallum \ (\ left (\ jobbra): \) \ [f „\ left (x \ right) \ le 0 \; \ forall \ ;. x \ in \ left (\ right) \] bizonyítjuk a tételt mindkét rész (szükséges és elégséges) esetén növekvő függvénye.

A szükséges feltétel.
Tekintsünk egy tetszőleges pont \ (\ a \ bal (\ jobbra). \) Ha a funkció \ (y = f \ left (x \ right) \) növekszik \ (\ left (\ jobbra), \), majd, definíció szerint lehet írni hogy \ [\ forall \ x \ in \ left (\ jobbra): x> \ Rightarrow f \ left (x \ right)> f \ left (> \ right); \] \ [\ forall \; x \ a \ left (\ right): x 0 \) mindenhol az intervallum \ (\ left (\ right) \), kivéve talán csak néhány kiválasztott pontokon, ahol \ (f \ left (x \ right) = 0, \ ), akkor a függvény \ (f \ left (x \ right) \) szigorúan növekvő.

Ennek megfelelően, a feltétel \ (f „\ left (x \ right) 0 \), akkor a függvény \ (f \ left (x \ right) \) szigorúan növekvő pontnál \ (\);

Ha a \ (f \ left (> \ right) 0 \) és \ (+ >> 0 \) (nem-negatív értékeket \ (x \) tartják a feltétel). Az eredmény: \ [-> \ right) \ left (+> \ right)> 0,> \; \;> \ right) - f \ left (> \ right)> 0.> \] Ez azt jelenti, hogy meghatározza a hogy a függvény \ (f \ left (x \ right) = + 1 \) egy szigorúan növekvő egy előre meghatározott intervallumban.

Találd meg az összes értékeket \ (a \), amelyre az egyenlet \ (- 6 + 9x + a = 0 \) három különböző valós gyöke.

A harmadfokú egyenlet határoz meg és differenciálható az egész számegyenesen. A származékot adják \ [- 6 + 9x + a> \ right) ^ \ prime >> = - 12x + 9.> \] egyenlővé a származék nullára, definiáljuk monotonitási időközönként funkció (ábra \ (15 \)): \ [\ ; \; - 12x + 9 = 0> \; \; - 4x + 3 = 0,> \; \; = 1 \; = 3> \]

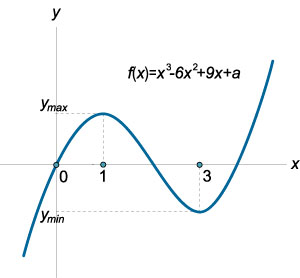
Így az átmenet (balról jobbra) a ponton át \ (x = 1 \) növekedése a funkció helyébe a csökkenést, azaz \ (X = 1 \) az a pont a maximum funkciót. Hasonlóképpen, \ (x = 3 \) az a minimális pontját a funkciót. A harmadfokú egyenlet lesz három különböző valós esetében a gyökereket ábrán látható \ (16 \). Maximum funkciót kell egy pozitív érték, és a minimális - negatív. Így érkezünk a következő feltételt: \ [\ left \<\begin y\left( 1 \right)> 0 \\ y \ bal (3 \ right) 0 \\ y \ bal (3 \ right) 0 \\ a - 4 \\ a 0. \) megoldása ezt az egyenlőtlenséget, kapjuk: \ [> \ cdot >> 0, > \; \; \ Right) \ left (\ right)> 0,> \; \; -> 0,> \; \; >> \; \; 16.> \]