Mi az EMA

3.3.Temperaturnoe területén folyamatos helyhez kötött pontforrás-Ni-ka egy végtelen közegben. Gauss hibafüggvény (EMA (x)).

Ha a pont-ke koordinátákkal x”. y”. z „időintervallumban a t” = 0 a t „= t RA-bot hőforrás teljesítmény W, a hőmérséklet területén az IP-pont-audio-ka, a fentiekben meghatározott, mo-Jette megtalálható integrálásával az alapvető megoldás a t” 0 és t (azaz, a bekapcsolási ig kikapcsolás). Keresse meg a származási koordináta azt a pontot, ahol a forrás TEP la. Ezután x '= y' = Z „= 0, és a képlet a hőmérséklet válik:

Azt, hogy az integrál (3.3.1) a változás a változók: r2 / [4a (t - t „)] = 2. Ezután: (t - t ') 3/2 = r3 / (8a3 / 23), dt' = r2d / (2a3). a határait integráció: t „= 0 

,t „= t   = . és esélyeket-mula (3.3.1) formáját ölti:

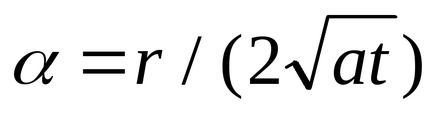
Az első szerves zárójelben, ismeretes a kurzus a magasabb matematika:

és a második integrál szempontjából elemi függvények nem lehet kifejezni, és meghatározza a különleges szórakoztató-to-tanulmányt, amely az úgynevezett Gauss-függvény hibát. vagy a beépített valószínűségét. vagy szórakoztató-to-chi-lány erfektum:

(Olvassa el az "erfektum" vagy rövidítve "ORF"). Ezzel a funkcióval a megoldást által kifejezett set-sok probléma, az elmélet a hővezetés, és más területeken a fizika fontos szerepet játszik.

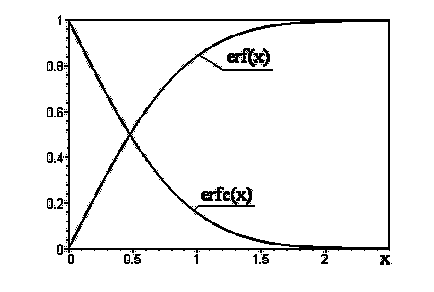
A meghatározás (3.3.3), hogy az EMA (0) = 0, és EMA () = 1, azaz a EMA (x) - egy Nem látom a-de-tone-de növekvő függvény megtekintéséhez egy raj izo keményforrasztás a 3.3 ábra. Funkció EMA (x) ta-bu-li - po-wang, és zna-cheniya átfutási ideje kemping Lich kormányzati segédkönyvek; 3.1 táblázat Az Island de nekünk néhány értékeket ezt a funkciót. Az előke-li-o-te-kah nem-to-toryh programozási nyelvek-CIÓ is egy-ményekről a pro-gram az Ön számára mi-Num-ment funkció EMA (x). Ha elkészíti a pro - gram, nincs, az EMA (x) függvény lehet you-Num-cast felhasználásával hatványsorba. "Mill-ajándék-t-ing", ha-lo-feszültség-CIÓ ezt a funkciót ste-pen-sósav szám, amely általában jelen van a matematikai-ches-cal Spra-Voch-tors, amelynek forma-:

E

A számos hasznos funkciók elemzésére tulajdonságait, de gyakorlati célokra is kényelmetlen, mert NE-váltakozó szeretné beállítani, hogy a számítások elvesztését eredményezi pontossággal. Kényelmesebb következik - fújás sorozat:

, .

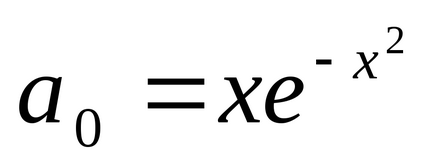
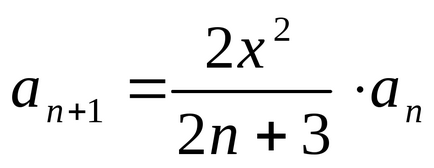
ez a szám elérte könnyedén csavarja programot vychisleniyaerf (x) a lu-bom nyelvi program-E CIÓ és da egy programozott mikro-kal-ku la tórusz. Az összegezés szükséges pre-él-Schat, CO-GDS hozzáadásával Oche-ed-de-edik idejének mennyiségben megállít-nyatsya (kell előre Stig-nu-ta "ma-gumiabroncs-értékű pontossággal").

Ha nagyobb pontosságra van szükség, akkor a közelítő odds-öszvér:

Formula (3.3.6) értékeit adja meg, az abszolút hiba, amely nem több, mint 6.310 -3. és otno-B Tel-értékű hiba nem több, mint 0,71%.

Néha, a negatív tartományban van szükség, hogy meghatározzuk EMA (x) x. Formula (3.3.3), nyilvánvaló, hogy az EMA (-x) = - EMA (x).

Megjegyezzük, hogy bár a funkció EMA (x) nem egy „elemi”, a szempontból CIÓ tulajdonságai és módszereket-Num-KÖZ ez könnyebb, mint a legtöbb „alapvető” funkciók, mint például a trigonometria.

Mivel a függvény EMA (x) kapcsolódó számos közös funkciót a hő-fi-kommunikáció-ches-cal problémákat. Ez elsősorban egy kiegészítő szerves ve-ro-Jat-ség:

amely akkor olyan gyakran, hogy egy speciális jel megszoktam: ERFC (x) (rövidítve olvasni „erfik”). A formája ez a funkció is ábrán látható 3.3.

Elég gyakran, a függvény EMA (x) meg kell különböztetni, és a-e-grirovat. Az op-re-de-ment (3.3.3) az következik, hogy

és a integrálja ERFC (x) (jelöljük ierfc (x)) egyenlő:

Visszatérve képletű (3.3.2). Megállapítva, hogy ca = . felírhatjuk ezt a képletet, mint:

Amikor t   függvény értéke

 0,  1 képletű és (3.3.10), mint amilyennek lennie kellene, cos pas da a képlet az álló megoldások (ha azt a T0 in-cha-lo-n, a referencia-RA-Tu ry), mert amikor t   előtt-STI-n-O-Xia-stacionárius eloszlása ​​pe-RA-A-ry határtalan közegben.

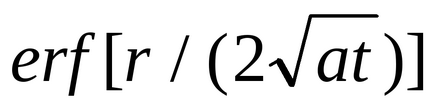
3.1 táblázat. Néhány függvény értékei EMA (x).