Tulajdonságok A szorzás természetes számok

Felszólították átfogó bemutatásának a szorzás a természetes számok. meg kell jegyezni, a találatok számát, specifikus erre a tevékenységre. Ezek az eredmények nevezzük inherens tulajdonságait szorzása természetes számok. Ebben a cikkben megmutatjuk néhány példát az alapvető tulajdonságait szorzás természetes számok, és azt írja a leveleket.

Oldalnavigáció.

Kommutativitás szorzás természetes számok.

Szorzás két egész szám van a kommutativitás. Itt a szövege tulajdonságok: A termék két egész szám nem változik, ha a permutációs szorzók helyeken. A leveleket a kommutativitás szorzás felírható: a · b = b · a. ahol a és b lehet bármilyen természetes számot (ha szükséges, lásd a cikk szó szerinti kifejezés).

Tekintsük a példát érvényességének megerősítését a kommutativitás szorzata két természetes számot. Jelentésén alapul szorzata két természetes számot. Kiszámítjuk a termék a 2. és 6., valamint a termék a számok 6 és 2, és ellenőrizze, hogy a szorzás eredménye. A termék a számok a 6. és a 2. összegével egyenlő 6 + 6. A felül táblázat 6 + 6 = 12. A terméket a 2. és 6. az összege 2 + 2 + 2 + 2 + 2 + 2. amely egyenlő a 12 (ha szükséges, lásd a cikk anyag és a további három több számot). Ezért, 6 × 2 × 2 = 6.

Szemléltető diagram a kommutativitás szorzata két természetes számot.

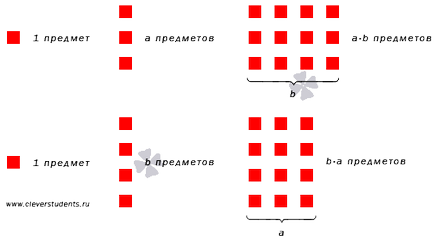
Asszociativitás szorzás természetes számok.

Nevezte az asszociativitás szorzata természetes számok: szorozza ezt a számot, a termék két szám - ugyanaz, mint ami a szaporodnak ez a szám az első tényező, és az eredményt megszorozzuk a második tényező. Azaz, a · (b · c) = (a • b) · c. ahol a. b és c lehet bármilyen természetes számok (zárójelben vannak zárva expressziós értékek számítása az első helyen).

Itt egy példa, hogy erősítse meg az asszociatív tulajdonságait szorzás természetes számok. Számítsuk ki a termék a 4 · (3 · 2). Értelmében a szorzás van 3 · 2 = 3 + 3 = 6. majd 4 + (3 × 2) = 4 × 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24. Most végre szorzás (4 * 3) · 2. Mivel 4 · 3 = 4 + 4 + 4 = 12. majd (3 · 4) = 12 · 2 · 2 = 12 + 12 = 24. Így, az egyenlőség 4 · (3 · 2) = (3 · 4) · 2. érvényességének megerősítését a szóban forgó ingatlan.

Megmutatjuk rajz szemlélteti asszociativitás szorzás természetes számok.

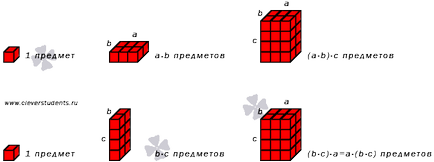
A rész lezárásához megjegyezzük, hogy az asszociatív tulajdonsága szorzás lehet egyedileg meghatározó szorzó három vagy több egész szám.

Forgalmazás és ingatlan szorzás felett tartjuk.

Az alábbi tulajdonság kötődik összeadás és szorzás. Ez az alábbiak szerint történik: szaporodnak ez az összeg két szám ezen a számon - ez ugyanaz, mint a hajtogatott termék az első ciklus, és az adott számot a termék a második tag, és a számot. Ez az úgynevezett elosztó tulajdonát szorzás felett tartjuk.

Íme egy példa igazolja a forgalmazás és ingatlan szorzás természetes számok. Mi érvényességének ellenőrzése egyenlet (3 + 4) = 2 · 3 · 2 + 4 · 2. Van (3 + 4) * 2 = 7 × 2 = 7 + 7 = 14. és 3 · 2 + 4 · 2 = (3 + 3) + (4 + 4) = 6 + 8 = 14. így, az egyenlet (3 + 4) = 2 · 3 · 2 + 4 · 2 igaz.

Azt állítjuk, a mintázat megfelel elosztó tulajdonában szorzás felett tartjuk.

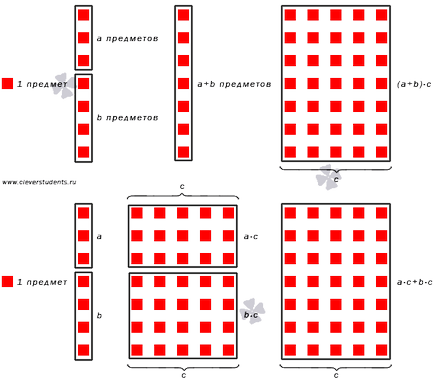
Forgalmazás és ingatlan szorzás tekintetében kivonás.

A szorzás és kivonás természetes számok kapcsolatos forgalmazás és ingatlan. Hangot adott készítmény: szaporodnak ez a különbség a két természetes számot adni egy természetes szám - olyan, mint a termék, és a csökkentett számú a kivonandó és vonjuk ki a termék számának.

Betűket használja elosztó tulajdonát szorzás tekintetében a kivonás felírható (a-b) · c = a · c-b · c. ahol a. b és c - természetes számok. Azáltal kommutativitás szorzás, a képlet is alkotnak · (b-c) = a • b-a · c.

Érvényességének ellenőrzése az elosztó tulajdonságainak szorzás tekintetében példáját kivonás. Mutassuk meg, hogy az egyenlő 3 * (4-2) = 3 · 4-3 · 2. Mivel 4-2 = 2 (ha szükséges, lásd a elmélet kivonás részegységhez a felül táblázatot), akkor a termék 3 · (4-2) egyenlő a termék a 3 · 2. és 3 x 2 = 3 + 3 = 6. Most nézzük különbség kiszámítására 3 · 4-3 · 2. Van 3 · 4-3 · 2 = (3 + 3 + 3 + 3) - (3 + 3) = 12-6 = 6. Így, a 3. egyenlet * (4-2) = 3 · 4-3 · 2 jobb.

egység tulajdonában szorzás egy természetes szám.

A következő ingatlan társított szorzó egység és egy természetes szám. Értelmében a szorzás, a termék az egység és a természetes szám n összegével egyenlő n kifejezések, amelyek mindegyike egyenlő eggyel. Következésképpen ,.

Például, a termék a számok 1 és 37 egyenlő 37; megszorozva az eredmény 1-es és 1004 száma 1004.

Másfelől, a termék n · 1 védjegy nem bír jelentéssel (abban az értelemben, a szorzás e munka az összege egy élettartama megegyezik az n szám. Addition de meghatároztuk két vagy több értelemben). Ahhoz, hogy továbbra is igaz, kommutativitás szorzás, azt feltételezzük, hogy a valódi egyenlőség n · 1 = n.

Például, a termék egyenlő 298 és 1 298 és ha szorozva 1. 71 megkapjuk 71.

Ilyenformán, a termék a két pozitív egész szám, amelyek közül az egyik egyenlő egy egyenlő egy másik számra. Az utolsó állítás megfogalmazása tulajdonságait szorzó egységek és egy természetes szám. A tulajdonság szorzás betűkkel írva: 1 · n = n · 1 = n. ahol n - bármilyen egész szám.

Szorzás tulajdonsága nulla egész szám.

Bár a nulla nem természetes szám, de még mindig a szorzás tulajdonsága a nulla és egy pozitív egész szám, akkor terjed ki ez a cikk. Ez annak a ténynek köszönhető, hogy ez a tulajdonság a szorzás a természetes számok oszlopban.

Ha ragaszkodunk az értelmét szorzás, a termék 0 · n. ahol n - tetszőleges természetes szám nagyobb, mint egy, az n az összege szempontjából, amelyek mindegyike nulla. Így. hozzátéve tulajdonságok lehetővé teszik számunkra, hogy azt állítják, hogy az utóbbi összeg nullával egyenlő.

Annak érdekében, hogy az érvényességét a tulajdonságait szorzás természetes számok az egység, amit arra az előző bekezdésben, figyelembe kell venni a helyes, a következő egyenlet 0 · 1 = 0.

Így minden olyan természetes szám n, a egyenlőség 0 · n = 0.

Ahhoz, hogy továbbra is igaz, kommutativitás szorzás is figyelembe egyenlőségét n · 0 = 0 minden n természetes szám.

Ilyenformán, a termék a nulla, és egy pozitív egész szám, értéke nulla. azaz 0 · n = 0 és n · 0 = 0. ahol n - természetes szám. Az utolsó állítás nyilatkozatot tulajdonságainak szorzás természetes számok és a nulla.

Összefoglalva, bemutatunk két példát kapcsolatos megérteni ezt a pontot szorzás tulajdonság. A termék a számok 45 és 0 nulla. 0 Ha megszorozzuk 45 970. Az a tény is, megkapjuk nulla.

Most már nyugodtan elkezdi tanulni a szabályokat, amelyek birtokában a szorzás a természetes számok.

• Matematika. Bármilyen tankönyvek 1, 2, 3, 4 különböző típusú oktatási intézmények.
• Matematika. Bármilyen útmutatók 5 osztály oktatási intézményekben.