Onnost funkció

Monoton függvény - egy funkció, amely nem változtatja meg a jel a növekmény, hogy mindig van egy nem-negatív, vagy nem pozitív mindig. Ha ráadásul a növekmény nem nulla, akkor a függvény az úgynevezett szigorúan monoton. Monoton függvény - olyan funkció, amely változik azonos irányban.

A funkció fokozott, ha egy nagyobb értéket az érv felel meg egy nagyobb a függvény értékét. Funkció csökken, ha a nagyobb érték az érvelés megegyezik a minimális érték a funkciót.

Hagyja az idő függvényében

funkció azt mondják, hogy egyre nagyobb az, ha

.

funkciót hívjuk szigorúan növekvő on, ha

.

funkciót hívjuk csökken a ha

.

funkciót hívjuk szigorúan monoton csökken a ha

.

(Szigorúan) növelésével vagy csökkentésével a funkciót nevezik (szigorúan) monoton.

A függvény y = f (x) nevezzük növekvő (csökkenő) egy bizonyos időközönként, ha x1 f (x2)).

Ha differenciálható függvénye y = f (x), az [a, b] nő (csökken) annak származékát ezen intervallumon f „(x)> 0

Ho pont az úgynevezett lokális maximum (minimum) az f (x), ha létezik egy olyan környéken, Ho, az összes pontot, ahol az egyenlőtlenség f (x) ≤ f (Ho) (f (x) ≥ f (Ho)).

Pont a legnagyobb és legkisebb szélsőérték nevezzük pontokat, és a függvény értékei ezeken a pontokon - a szélsőségek.

Szükséges feltételeket extrémuma. Ha Ho egy pont szélsőérték az f (x), akkor vagy f „(Ho) = 0 vagy F (Ho) nem létezik. Az ilyen pontokat nevezzük kritikus és a funkció határozza meg a kritikus pontot. Szélsőséges funkciók között megtalálhatók a kritikus pontokat.

Az első feltétel elegendő. Let Ho - a kritikus pont. Ha f „(x), amikor áthalad a ponton Ho változik jele a plusz mínusz, majd azon a ponton, Ho funkció maximum, egyébként - legalábbis. Ha átmegy a kritikus pont a származék nem változik jel, akkor azon a ponton, Ho nincs szélsőérték.

A második elégséges feltétel. Tegyük fel, hogy az f (x) a származék f „(x) a szomszédságában Ho és második derivált a ponton Ho. Ha f „(Ho) = 0,> 0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

Az [a, b] az y = f (x) elérheti a legkisebb vagy a legnagyobb értéket, vagy a kritikus pontokat vagy szegmensek végein [a, b].

7.Intervaly konvex, konkáv függvény olvadási inflexiós.

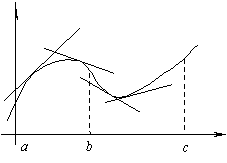
A grafikon y = f (x) azt mondják, hogy konvex intervallumban (a; b). ha úgy helyezkedik alacsonyabb, mint bármelyik érintőleges ebben az intervallumban.

A grafikon y = f (x) az úgynevezett homorú az intervallum (a; b). ha bármelyik való érintkezési ebben az intervallumban.

Az ábra azt mutatja, a görbe, domború (a; b) és konkáv (b, c).

Félkör konvex [-1; 1].

A parabola y = x2 konkáv az intervallum (-∞; + ∞).

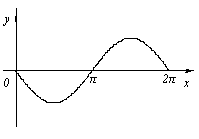
Ütemezés funkció az azonos időközönként lehet konvex, és a másik konkáv. Mivel a grafikon y = sin x [0,2; π], domború az intervallumban (0; π) és egy homorú (π; 2π).

Tekintsük elegendő kritérium, amely lehetővé teszi, hogy meghatározzuk, hogy a funkció diagram a tartományban konvex vagy konkáv.

Tétel. Tegyük fel, y = f (x) differenciálható (a; b). Ha az összes pontot az intervallum (a; b) a második függvény deriváltját y = f (x) negatív, azaz f '' (x) <0, то график функции на этом интервале выпуклый, если же f ''(x )> 0 - homorú.

Bizonyítás. Azt feltételezzük, a meghatározottsága, hogy f „” (x) <0 и докажем, что график функции будет выпуклым.

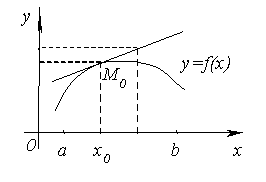
Tekintsük a gráf függvénnyel y = f (x) a tetszőleges pont abszcissza M0 x0  (a; b) és felhívni érintőjének a ponton át M0. A egyenletet. Megmutatjuk, hogy a grafikon a funkció (a; b) ez alatt az érintőleges, azaz egy és ugyanazt az értéket x ordináta a görbe y = f (x) kisebb, mint az ordinátán tangensét.

függvény inflexiós pont

Ebben a kifejezést, vannak más célra, lásd. Az inflexiós pontot.

Az inflexiós pont meghatározási funkció belső tochkaoblasti ilyen chtonepreryvna ezen a ponton, van egy véges vagy végtelen származékot határoztuk karakter ezen a ponton, mind vége iyavlyaetsya szigorú domborulata az intervallumot és a start-up intervallum szigorú konvexitás lefelé, vagy fordítva.

Ebben az esetben, yavlyaetsyatochkoy inflexiós pont a függvény grafikon, azaz, a grafikon a funkció „dől” cherezkasatelnuyu rá ezen a ponton: ha egy érintője a grafikon alatt, és pri- a grafikon fölött (vagy fordítva)

Ennek szükséges feltétele, hogy létezik egy inflexiós pont, ha az f (x), kétszer differenciálható a szomszédságában a inflexiós pont van vtochku majd.

Egy elégséges feltétel, hogy létezik egy inflexiós pont, ha a funkció egy olyan környéken tochkiraz folytonosan differenciálható, és prichemnechotno, és ahol egy, funktsiyaimeet vtochku inflexiós.