Online kalkulátor - kiszámítani a határozott integrál (ívelt területe trapéz)

Ez a matematikai számológép online segít kiszámítani a határozott integrál (terület a görbe vonalú trapéz). Program kiszámítja a határozott integrál (terület a görbe vonalú trapéz) nem csak megadja a választ a problémára, az eredmény egy részletes megoldást magyarázatot. azaz Ez azt mutatja, a folyamat integrálása a funkciót.

Hasznos lehet a diákoknak a vezető osztályok középiskolák felkészülés tesztek és vizsgálatok, ellenőrzések tudás a vizsga előtt, a szülők figyelemmel kíséri a megoldást sokan matematika és algebra problémákat. Vagy talán túl drága bérelni egy tanár, vagy vásárolni az új könyveket? Vagy csak szeretne a lehető leggyorsabban kell csinálni a házi feladatot a matematika vagy algebra? Ebben az esetben, akkor is kihasználják a programok részletes megoldásokat.

Így lehet végezni a saját képzési és / vagy oktatási azok fiatalabb testvére ugyanazon a szinten az oktatás területén a feladatok növekedésével.

mert hajlandó megoldani a problémát nagyon sok, a kérés sorban áll.
Néhány másodperc múlva az oldatot jelennek meg.
Kérjük, várjon egy percet. Nem akarom, hogy várjon!

Ezek a megoldások jönnek létre, és tárolja a felhasználók által a szerverünkön
ezzel az online kalkulátor.

A határozott integrál.
Vezető problémák a koncepció a határozott integrál

1. feladat (kiszámításához a területet a görbe vonalú trapéz).

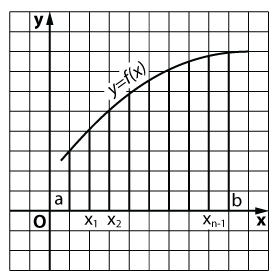
A Descartes-féle koordináta-rendszer XOY adott ki (lásd. Ábra) által határolt az x tengely, az egyenes vonalak x = a, X = b (a

A koncepció a határozott integrál

Adunk egy matematikai leírását a modell, amely-ben épült három feladatot tekinthető egy függvény y = f (x), a folyamatos (de nem feltétlenül nem-negatív, mint feltételezték a problémák figyelembe), az [a; b]:
1) osztott, az [a; b] n egyenlő részre;
2) az az összeg,

3) kiszámítása

Ennek során a matematikai analízis bizonyította, hogy ez a határérték esetén folyamatos (vagy darabot-bölcs folytonos) függvény létezik. Ezt nevezik a határozott integrál egy függvény y = f (x) felett, az [a; b], és a következőképpen jelöljük:

A és b számok nevezzük határain integrációs (rendre alsó és felső).

Térjünk vissza az előbb említett probléma. A terület meghatározása megadott 1. probléma most újraírni az alábbiak szerint:

Itt S - területe görbe vonalú trapéz látható a fenti ábrán. Ez a geometriai jelentése a határozott integrál.

Meghatározása az elmozdulás s egy pont mozog egy egyenes vonal sebességgel v = v (t), egy időintervallum t = a t = b, megadott Probléma 2 lehet átírni:

Newton formula - Leibniz

Ahhoz, hogy elkezdjük megválaszolni a kérdést: mi az összefüggés a határozott integrál és a primitív?

A válasz megtalálható feladat 2. Egyrészt, az elmozdulás s egy pont mozog egy egyenes vonal sebességgel v = v (t), az időintervallum a t = a, és t = b, kiszámítása az alábbi képlet szerint

Másrészt, a koordináta pont mozog primitív sebesség - jelöli annak S (t); azt jelenti, a mozgás által kifejezett általános képletű s s = s (b) - s (a). Ennek eredményeképpen megkapjuk:

ahol s (t) - primitív v (t).

Ennek során a matematikai analízis bebizonyította a következő tétel.
Tétel. Ha a függvény az y = f (x) folytonos intervallumon [a; b], majd a következő képlet

ahol F (x) - primitív f (x).

A fenti képlet általában úgynevezett Newton formula - Leibniz után az angol fizikus Isaaka Nyutona (1643-1727) és a német filozófus Gottfried Leibniz (1646- 1716), kapott függetlenül és gyakorlatilag egyszerre.

A gyakorlatban, írása helyett F (b) - f (a) alkalmazunk bejegyzés (néha úgynevezett kettős helyettesítés), és ennek megfelelően, átírni Newton képletű - Leibniz formájában:

Kiszámítása határozott integrál, először meg egy primitív, majd kétszer helyettesítés hajtódik végre.

Képlet alapján Newton - Leibniz, ez lehetséges két tulajdonsága a határozott integrál.

Az ingatlan 1 integrál összege funkciók összegével egyenlő az integrálok:

Az ingatlan 2 állandó tényező lehet kivinni az integrál jel:

Kiszámítása területek síkidomok révén határozott integrálok

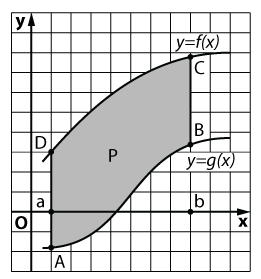
A szerves ki lehet számítani a terület nem csak a görbe vonalú trapéz, de síkidomok egy még összetettebb formáját, mint például a ábrán látható. Ábra F által határolt sor x = a és x = b és diagramok folyamatos funkció y = f (x), y = G (x), ahol az intervallum [a; b] egyenlőtlenség. Számítani a területet S a szám, amit a következőképpen jár el:

Tehát, az S felület alakja, által határolt sor x = a és x = b és grafika függvény az y = f (x), y = G (x), a folyamatos intervallumon [a; b] és olyan, hogy minden x intervallumban [a; b] egyenlőtlenség képlettel számítottuk ki

Táblázat határozatlan integrálok (primitívek) bizonyos funkciók

$$ \ int 0 \ cdot dx = C $$

$$ \ int 1 \ cdot dx = x + C $$