Mi a monoton függvény 1

1.3.5. monoton függvények

f (x) függvény az úgynevezett távolság növelésével D. Ha bármilyen egész szám x 1 és x 2 a különbség a D, oly módon, hogy x 1

f (x) függvény, csökken a rés D. Ha bármilyen egész szám x 1 és x 2 a különbség a D, oly módon, hogy x 1 f (x 2).

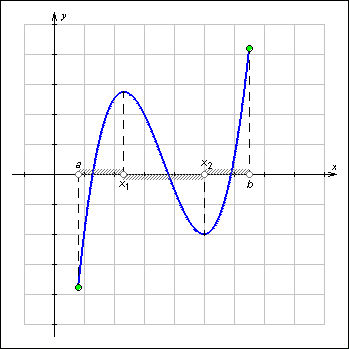
Időközönként növekedését és csökkenését funkció

Az ábrán bemutatott grafikont függvény az y = f (x). növeli az egyes intervallumok [a; x 1) és a (X 2; b] és csökkenti a rés (x 1; x 2). Megjegyezzük, hogy a funkció növeli az egyes intervallumok [a; x 1) és a (X 2; b], de nem kombinációban. rések

Ha a függvény növekszik vagy csökken bizonyos időközönként, akkor az úgynevezett monoton ezen intervallumban.

Jegyezzük meg, hogy ha f - egy monoton függvény az intervallum D (f (x)). egyenlet f (x) = const lehet több, mint egy gyökér ebben az intervallumban.

Valóban, ha x 1

Mi listát tulajdonságait monoton függvény (feltételezzük, hogy minden funkcióját meghatározni egy bizonyos időközönként D).

• Az összeg több növekvő függvények növekvő függvénye.
• Artwork nemnegatív növekvő függvény növekvő függvénye.
• Ha az f függvény növeljük, akkor a funkciók cf (c> 0) és az f + C is növeli, és a funkciót cf (c <0) убывает. Здесь c – некоторая константа.
• Ha f növekszik, és megtartja jel, a funkció 1 / f csökken.
• Ha az f függvény növekszik, és nem negatív, akkor hol. is növeli.
• Ha f növekszik, és az N - páratlan, akkor f n is növeli.
• Összetétel g (f (x)) növekvő f és g függvények is növeli.

Hasonló megállapításokat lehet kiszerelni csökkenő függvény.

Model 1.9. tulajdonságait a funkció

egy pontot nevezzük, legfeljebb az f függvény. ha van egy ε-szomszédságában a. hogy az egyenlőtlenség f (a) ≥ f (x) minden x ettől a környéken.

Egy pont az úgynevezett pontja minimum az f függvény. ha van egy ε-szomszédságában a. hogy minden x ebben a környéken egyenlőtlenség f (a) ≤ f (x).

Az a pont, ahol a maximális vagy minimális a funkció, az úgynevezett szélsőérték pont.

A lényeg a szélsőérték változás a karakter monotonitás. Tehát, hogy a bal oldalon a pont szélsőérték funkció növelheti, és a jog - csökken. A definíció szerint a extremális pont kell egy pont a tartományon belül.

Ha bármilyen (x ≠ a) a következő egyenlőtlenség f (x) ≤ f (a), akkor a pont az úgynevezett egy pont a maximális értékei a beállított D.

Ha bármilyen (x ≠ b) a következő egyenlőtlenség f (x)> f (b) a b pont egy pont a legkisebb érték a beállított D.

a legmagasabb vagy legalacsonyabb értékek egy pont lehet szélsőérték funkció, de nem feltétlenül az.

Legmagasabb pont (legkisebb) értéke a folytonos függvény az intervallumon között található szélsőértékében ezt a funkciót, és annak értékeit a végpontokat.