Kalkulátor Online - határozat logaritmikus egyenletek

Ez a matematikai számológép az online, hogy segítsen megoldani a logaritmikus egyenlet. Program megoldására logaritmikus egyenletek nem csak ad választ arra a problémára, az eredmény egy részletes megoldást magyarázatot. azaz Ez azt mutatja, a folyamat kezd egy választ.

Hasznos lehet a diákoknak a vezető osztályok középiskolák felkészülés tesztek és vizsgálatok, ellenőrzések tudás a vizsga előtt, a szülők figyelemmel kíséri a megoldást sokan matematika és algebra problémákat. Vagy talán túl drága bérelni egy tanár, vagy vásárolni az új könyveket? Vagy csak szeretne a lehető leggyorsabban kell csinálni a házi feladatot a matematika vagy algebra? Ebben az esetben, akkor is kihasználják a programok részletes megoldásokat.

Így lehet végezni a saját képzési és / vagy oktatási azok fiatalabb testvére ugyanazon a szinten az oktatás területén a feladatok növekedésével.

log (b) vagy a log (e, b) - a természetes alapú logaritmusa b
log (10, b) - a logaritmus b
log (a, b) - a logaritmusát a b a bázis egy

mert hajlandó megoldani a problémát nagyon sok, a kérés sorban áll.
Néhány másodperc múlva az oldatot jelennek meg.
Kérjük, várjon egy percet. Nem akarom, hogy várjon!

Ezek a megoldások jönnek létre, és tárolja a felhasználók által a szerverünkön
ezzel az online kalkulátor.

Logaritmikus függvény. logaritmusok

Probléma 1. Keresse meg a pozitív gyöke az egyenletnek x 4 = 81
A definíció szerint van gyökér aritmetikai \ (x = \ sqrt [4] = 3 \)

Probléma 2. egyenlet megoldásához 81 x = 3
Írunk az egyenlet a következő: x = 3 4 3 x = 4

Az 1. feladat ismeretlen bázis mértékben és a probléma 2 - kitevő. 2. A módszer a probléma megoldására, az volt, hogy a bal és a jobb oldalon az egyenlet ábrázolható, mint egy, mint az azonos alap 3. De például a 3. egyenlet x = 80 ilyen módon nem lehet megoldani. Azonban ez egyenletnek gyöke. Ahhoz, hogy megoldja ezeket egyenletek bevezetik a logaritmusát a számot.
Egyenlet a x = b, ahol a> 0, \ (a \ NEQ 1 \), b> 0, egy egyedi gyökér. Ez gyökér nevezik logaritmusa b nincs alapja, és egy kijelölt loga b
Például, a gyökér a egyenlet 81 x = 3 a szám 4, azaz a, log3 4 = 81.

Definíció. Logaritmusa pozitív számot bázis b a, ahol a> 0, \ (a \ neq 1 \) az úgynevezett kitevő, hogy növelni akarja a szám egy, hogy b

log2 8 = 3, mert 2 3 = 8

log7 7 = 1, mivel a 7 = 7 1

Meghatározása a logaritmus felírható:

Ez az egyenlet érvényes b> 0, b> 0, \ (a \ neq 1 \). Ez általában a továbbiakban a fő logaritmikus identitását.

Az akció a megállapítás a logaritmusa hívott szám a logaritmus.
Az akció számának meghatározásánál a logaritmus hívják hatás.

Számítsuk log64 128
Legyen x = log64 128. A meghatározás szerint a 64 logaritmusa x = 128. Mivel 64 = 2 6. 128 = 2 7. 2 a 6x = 7. 2 6x = 7, X = 7/6.
Válasz log64 128 = 7/6

Számítsuk \ (^ 3 \)
Az ingatlan és mértéke az alap logaritmikus identitás, azt látjuk,

Problémák egyenletet log3 (1-x) = 2
A definíció logaritmusa március 2 = 1 - x, ahol x = -8

A tulajdonságait logaritmus

Amikor az átalakulások tartalmazó kifejezések a logaritmus, a számításokat és az egyenletek megoldására különböző tulajdonságokkal gyakran használják a logaritmus. Tekintsük a legfontosabbak.

Tegyük fel, hogy a> 0, \ (a \ NEQ 1 \), b> 0, c> 0, R - bármely valós szám. Ezután a következő képlet:

2) \ (\ log_a \ frac = \ log_a b - \ log_a c \)

Tizedes és természetes alapú logaritmus

Mert logaritmusainak szám készült különleges asztalok (táblázatok logaritmus). Logaritmusok számítása szerint a számológép. Ebben és a másik esetben csak decimális vagy természetes logaritmusa.

Definíció. Decimális számának logaritmusával nevezzük számának logaritmusával bázis-10 és írásbeli
lg b helyett log10 b

Definíció. A természetes logaritmusa hívott szám logaritmusát a számot a bázis e, ahol e - irracionális szám, megközelítőleg egyenlő 2,7. Ha ez a leírás ln b helyett Loge b

Irracionális szám e fontos matematika és alkalmazásai. Az e szám felírható az összege:
$$ e = 1 + \ frac + \ frac + \ frac + \ dots + \ frac + \ dots $$

$$ e \ kb 2,7182818284 $$

Kiderült, hogy ez elegendő ahhoz, hogy tudja, csak a tizedes értékeket, vagy csak a természetes logaritmusa számok, hogy megtalálják a logaritmusa számok bármilyen okból.
Erre a célra csere a logaritmus alap képlet:

ahol b> 0, a> 0, \ (a \ NEQ 1 \), c> 0, \ (c \ NEQ 1 \)

Következményei általános képletű helyettesítő logaritmus alapja.
Ha c = 10, és c = e nyert Formula átmenet decimális logaritmus és természetes:
$$ \ log_a b = \ frac. \; \; \ Log_a b = \ frac $$

Logaritmikus függvény, annak tulajdonságait és a menetrend

A matematika és alkalmazásai közös logaritmikus függvény
y = loga x
és ahol - az előre meghatározott számú, a> 0, \ (a \ NEQ 1 \)

A logaritmikus függvény a következő tulajdonságokkal rendelkezik:
1) A domain a logaritmikus függvény - a készlet minden pozitív egész szám.

2) A beállított értékek logaritmikus függvény - a készlet minden valós számok.

3) A logaritmikus függvény nem korlátozott.

4) A logaritmikus függvény az y = loga x az, hogy növeli a intervallumot \ ((0; + \ infty) \), ha a> 1,
és csökkenő, ha 0 1, akkor a függvény az y = loga x pozitívnak x értéke> 1,
negatív 0 1.

Oy tengelye függőleges aszimptotájának a grafikon y = loga x

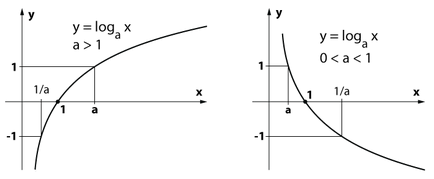
Megjegyezzük, hogy minden gráf a logaritmikus függvény az y = loga x áthalad a ponton (1; 0).
Az egyenletek megoldására gyakran használják a következő tétel:

A logaritmikus függvény az y = loga x és az exponenciális függvény az y = A x. ahol a> 0, \ (a \ NEQ 1 \) kölcsönösen inverz.

logaritmikus egyenletek

Problémák egyenletet log2 (x + 1) + log2 (x + 3) = 3
Tegyük fel, hogy x - egy szám, amelynél a egyenlőség igaz, vagyis, x - a gyökere az egyenlet. Ezután a tulajdonsága logaritmusa közötti egyenlőség
log2 ((x + 1) (x + 3)) = 3
Ebből az egyenletből, hogy meghatározzák a logaritmus megkapjuk
(X + 1) (x + 3) = 8
x 2 + 3 + 4 = 8, azaz x 2 + 4x - 5 = 0, x1 = 1, x2 = -5
Mivel a másodfokú egyenlet következménye az eredeti egyenlet, akkor ellenőrizni kell.
Ellenőrzésére, hogy a számok 1 -5 és gyökerek az eredeti egyenlet.
Behelyettesítve a bal oldalon a kezdeti egyenlet x = 1, megkapjuk
log2 (1 + 1) + log2 (1 + 3) = log 2 2 + log2 4 = 1 + 2 = 3, azaz a X = 1 - a gyökere az egyenlet.
Amikor x = -5 + 1 számú x + 3, és x negatív, és ezért a bal oldalon az egyenlet nincs értelme, azaz = -5 x nem gyökér ennek az egyenletnek.
A válasz X = 1

Lg megoldani egyenlet (2x 2 - 4x + 12) = lg x + lg (x + 3)
Az ingatlan logaritmus
lg (2x 2 - 4x + 12) = lg (x 2 + 3x)
ahonnan
2 2x - 4x + 12 = x 2 + 3x
x 2 - 7x + 12 = 0
x1 = 3, x2 = 4
Vizsgálatok azt mutatják, hogy a két x értékei a gyökerei az eredeti egyenletnek.
Response x1 = 3, x2 = 4

Problémák egyenletet log4 (2x - 1) • log4 x = 2 log4 (2x - 1)
Nézzük át ezt egyenletet:
log4 (2 * - 1) • log4 x - 2 log4 (2 * - 1) = 0
log4 (2x - 1) • (log4 x - 2) = 0
Egyenlővé minden tényező a bal oldalon az egyenlet nulla, ezt kapjuk:
1) log4 (2 - 1) = 0, ahol a 2 - 1 = 1, x1 = 1
2) log4 x2 = 0 ahol log4 = 2, x2 = 16
Vizsgálatok azt mutatják, hogy a két x értékei a gyökerei az eredeti egyenletnek.
Válasz x1 = 1, x2 = 16

Könyvek (könyv) Könyvek (mások) Abstracts vizsga és OGE tesztek online játékok, kirakós játékok rajzoló funkciókat szótár ifjúsági szleng katalógus iskolák Magyarországon Termék SSUZov Magyarország Directory Magyarország egyetem problémák megtalálása GCD és LCM egyszerűsítése polinom (polinom szorzás) Division polinom egy polinom oszlop számítása numerikus frakciókat problémák megoldása százalékban komplex számok: összege, különbség, a termék és a hányadost rendszerek 2 lineáris egyenletek két változó Megoldás a másodfokú egyenlet Bold négyzet dvuch Lena és faktoring másodfokú polinom határozat egyenlőtlenségek határozat egyenlőtlenségek grafikai rendszer kvadratikus Függvényábrázolásnál lineáris frakcionált funkció megoldja számtani és mértani sorozat döntést trigonometrikus, exponenciális, logaritmikus egyenletek határértékeinek kiszámítására, származék, tangens szerves primitív oldatot háromszögek Számítások cselekvések vektorokkal Számítások akció vonal és sík terület geometriai formák geometriai alakzatok határoló em geometriai formák felülete geometriai formák
Tervező vezetési helyzetekben
Időjárás - Hírek - horoszkóp
MathSolution.ru programot a Google Playen