Határozott integrál és számítási módszereket
Határozott integrál egy folytonos függvény f (x) egy véges intervallumon [a. b] (ahol) a növekménye annak néhány primitív ebben a szegmensben. (Valójában, a megértés sokkal könnyebb, ha ismételt téma határozatlan integrál) Ezt a rekordot használják
Amint az alsó kör (növekmény primitív függvény kijelölt) meghatározott szerves lehet pozitív vagy negatív szám (különbségként számítjuk közötti az értéke egy primitív a felső határ, és ez az érték az alsó határ, t. E. egy F (b) - F (a)).
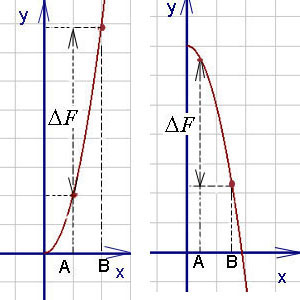
Az a és b számok nevezzük az alsó és a felső határértékek az integráció, és a szegmens [a. b] - az intervallum az integráció.
Így, ha F (x) - bármilyen primitív függvény f (x), akkor értelemszerűen,
Egyenlet (38) van kifejezve a Alapvető Newton. A különbség F (b) - f (a) van rögzítve röviden a következő:
Ezért a Newton-Leibniz formula lesz írva így:
Mi bizonyítja, hogy a határozott integrál nem függ attól, hogy a primitív az integrandus venni, amikor azt értékeljük. Legyen f (x) és az F (x) - tetszőleges primitívek integrandust. Mivel ez a primitívek az azonos funkciókat, akkor különböznek egy konstans kifejezés: F (x) = f (x) + C. Ezért,
Ez azt igazolja, hogy az intervallum [a. b] megnöveli az összes primitívek f (x) egybeesik.
Így, hogy kiszámítja a határozott integrál szükséges találni olyan primitív integrandusz, azaz először meg kell találni a határozatlan integrál. A C konstans, a későbbi számítások kizárt. Ezután Alaptételének képlet alkalmazható: egy primitív függvény helyett a felső határ b. a továbbiakban - az alsó határértéket, és számolt különbség F (b) - F (a). Az eredményül kapott szám a határozott integrál.
Ha a = b, definíció szerint, figyelembe
Annak érdekében, hogy gyakorlat megtalálása határozott integrálok szüksége van egy táblázat az alapvető határozatlan integrálok és előnyök „Műveletek és hatáskörrel gyökereit.”
Példa 1. Számítsuk ki a határozott integrál
Határozat. Először is, meg határozatlan integrál:
Alkalmazása Alaptételének primitív
(Ha C = 0), megkapjuk
Kiszámítása során azonban a határozott integrál jobb nem lehet egy külön primitív és szerves rekord azonnal formájában (39).
Ellenőrizze a megoldás lehet a kalkulátor vonal határozatlan integrálok a számítás eredményeit primitív helyettesítő első felső határérték és az alsó határérték és keresse meg a különbséget. Az eredményül kapott szám a határozott integrál.
Példa 2. Számítsuk ki határozott integrál
Határozat. a következő képlet segítségével
Ellenőrizze a megoldás lehet a kalkulátor vonal határozatlan integrálok a számítás eredményeit primitív helyettesítő első felső határérték és az alsó határérték és keresse meg a különbséget. Az eredményül kapott szám a határozott integrál.
Tétel 1.Opredelonny egybeépített ugyanezen korlátok integrációs nulla. azaz
Ez a tulajdonság meghatározásában szereplő a határozott integrál. Azonban, ez is előállíthatók a Newton-Leibniz formula:
Tétel 2.Velichina határozott integrál nem függ a kijelölés a változó az integráció. azaz
Legyen f (x) - a primitív f (x). Az F (t) a primitív az azonos funkciót F (t), ahol az egyetlen független változó nem jelezzük. ezért
Alapján a (39), az utolsó egyenlőség egyenlő integrálok
Tétel 3.Postoyanny tényező lehet venni, mint egy jel a határozott integrál. azaz
Tétel 4.Opredelonny integrál algebrai összege véges számú funkciókat egyenlő az algebrai összege integrálok egyes ezeket a funkciókat. azaz
5. Tétel Ha a szegmens az integráció részekre van osztva, akkor a határozott integrál időintervallumra összegével egyenlő határozott integrálok részei. azaz ha
Tétel 6. Amikor permutáció integráció korlátozza az abszolút értéke a határozott integrál nem változik, csak megváltoztatja jel. azaz
Tétel 7 (a középérték-tétel). Határozott integrál egyenlő a termék hosszának integrációs intervallum értéke az integrandus egy bizonyos ponton belül. azaz
Tétel 8. Ha a felső határa az integráció és nagyobb, mint az alsó integrandus nemnegatív (pozitív), akkor u nemnegatív határozott integrál (pozitív), azaz ha
Tétel 9. Ha a felső határa az integráció és nagyobb, mint az alsó és a folytonos függvény, akkor a egyenlőtlenség
Meg lehet integrálni Terminusonként. azaz
Az ingatlan a határozott integrál lehetővé teszi számunkra, hogy egyszerűsítse a közvetlen kiszámítása integrálok.
Példa 3. Számítsuk ki a határozott integrál
Használata 3. és 4. Tétel, és amikor a primitívek - táblázatos integrálok (7) és (6), megkapjuk
Ellenőrizze a megoldás lehet a kalkulátor vonal határozatlan integrálok a számítás eredményeit primitív helyettesítő első felső határérték és az alsó határérték és keresse meg a különbséget. Az eredményül kapott szám a határozott integrál.
Legyen f (x) - folyamatos intervallumban [a. b] funkciót, és az F (x) - a primitív. Tekintsük a határozott integrál
és T jelentése változó az integráció, hogy ne keverjük össze a felső határ. Ha x változik és változások opredolenny integrál (47), azaz a ez függvénye a felső határ integráció x. amely jelöli F (x), azaz
Megmutatjuk, hogy a F (x) egy primitív f (x) = f (t). Valóban, differenciáló F (x), megkapjuk
A F (x) - egy a végtelen számú primitívek a f (x), nevezetesen azt, hogy ami x = a nulla. Ez a jóváhagyás kapunk, ha a (48), hogy x = a és használja 1. Tétel az előző bekezdés.
Származtatására a képlet integrálás egyenlettel u dV = d kaptunk (UV) - v du. Integrálása a tartományban a B és figyelembe 4. tétel bekezdése ezt a cikket a tulajdonságait a határozott integrál, megkapjuk
Amint következik Tétel 2 szakaszt a tulajdonságait a határozatlan integrál, az első kifejezés a jobb oldalon egyenlő a különbségi értékek a termék UV a felső és alsó határértékek az integráció. Írásban ezt a különbözetet röviden
Kapjuk részekkel integráció formula, hogy kiszámítsa a határozott integrál:
4. példa Számítsuk ki a határozott integrál
Határozat. Integrálása az alkatrészek, figyelembe véve u = ln x. dv = dx; majd du = (1 / x) dx. v = x. A képlet (49) találunk
Ellenőrizze a megoldás lehet a kalkulátor vonal határozatlan integrálok a számítás eredményeit primitív helyettesítő első felső határérték és az alsó határérték és keresse meg a különbséget. Az eredményül kapott szám a határozott integrál.
Térjünk át a kiszámítására határozott integrál megváltoztatásával változtatható. enged
ahol, definíció szerint, F (x) - primitív f (x). Ha egy helyettesítő változót a integrandust
képlet szerinti (16) felírható
Ebben a kifejezésben,
primitív függvény
Valójában, annak származéka, a szabály alapján a differenciáló összetett funkció
Tegyük fel, hogy α és β - értéke a t változó. amelyre a függvény
Tart az értékeket a és b. azaz
De, az alábbi képlet szerint Alaptételének, a különbség F (b) - F (a)
Ez a képlet az átmenetet egy új változó jel alatt a határozott integrál. Vele, a határozott integrál
váltás utáni változó
alakítható határozott integrált képest az új változó t. Ebben az esetben a régi határait integráció és b helyébe újak és kívül. , Meg kell találni egy egyenlet új határértékek
ellátási értékek x = a és x = b. azaz egyenletek megoldására
és relatív. Miután megtalálta a új határértékeket az integráció számítás a határozott integrál csökken a használata a Alaptételének képletű a szerves az új változó t. A primitív függvény, amely eredményeként kapott a megállapítás a szerves vissza a régi változó nem szükséges.
Kiszámításakor a határozott integrál a változó csere módszer gyakran célszerű kifejezni nem a régi változó függvényében az új, hanem egy új - a régi funkciót.
5. példa Számítsuk ki a határozott integrál
Határozat. Proizvedom változás változó, feltételezve,
Ezután dt = 2x dx. ahol x dx = (1/2) dt. és az integrandus átalakul a következőképpen:
Találj új határértékek az integráció. Behelyettesítve x értékei = 4 és X = 5 az egyenletben
Most a következő képlet segítségével (50), megkapjuk
Miután a változás a változó, akkor nem tért vissza a régi változót, és használta a Newton-Leibniz formula a kapott primitív.
Ellenőrizze a megoldás lehet a kalkulátor vonal határozatlan integrálok a számítás eredményeit primitív helyettesítő első felső határérték és az alsó határérték és keresse meg a különbséget. Az eredményül kapott szám a határozott integrál.
Kezdés téma „Integrál”