folytonosság funkció

A koncepció egy folytonos függvény matematikai érkezik, előbb tanulmányozza a különböző törvények a mozgás. Idő és tér végtelen, és a függőség, például az út s az idő t. kifejezett jog s = f (t). Ez ad egy példát egy folytonos függvény f (t). Folyamatosan változik, és a hőmérséklet a felmelegített víz, ez is egy folytonos az idő függvényében: T = f (t). Folytonos vonal, és ha lehet levonni felemelése nélkül ceruzát a papírról. Ez a vonal a grafikon egy folytonos függvény.

Grafikailag a függvény folytonos egy ponton, ha a grafikon nem „működik” ezen a ponton. A grafikon folytonos függvény - az alábbiakban látható.

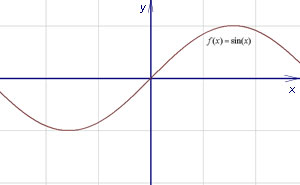
Meghatározása folytonosság funkciót limit. A függvény folytonos a ponton három feltétel:

1. A funkció meghatározott pontban.

2. Van egy határ függvény egy pontban, a jobb és bal határok egyenlő.

3. Az limit funkció egy ponton megegyezik a függvény értéke ezen a ponton:

Ha legalább az egyik a fenti feltételek nem teljesülnek, a funkció nem folyamatos a ponton. Ugyanakkor azt mondja, hogy a függvény nem folytonos, és a pontokat a grafikont, amelyben a menetrend megszakad, az úgynevezett pontok abbahagyni. A grafikon egy ilyen függvény, Brooks diszkontinuitás az x = 2 - az alábbiakban.

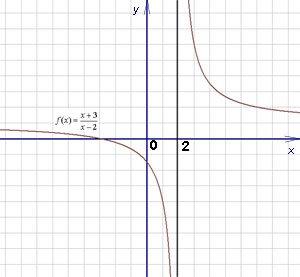
1. példa f (x) függvény meghatározása a következő:

Függetlenül attól, hogy ez a függvény folytonos az egyes határpont ágainak, azaz azokon a pontokon x = 0 x = 1. X = 3?

Határozat. Mi ellenőrizze mindhárom feltétel folytonosságának a függvény minden határpont. Az első feltétel teljesül, mivel ezt a funkciót definiáljuk az egyes határpont következik a meghatározása a funkciót. Továbbra is, hogy ellenőrizze a másik két feltétel.

X = 0 Találunk egy bal határ ezen a ponton:

Keressen egy jobb oldali korlát:

A határérték funkciója és a függvény értéke a ponton x = 0 kell találni az ágak a funkciót, amely magában foglalja ezt a pontot, azaz a második ága. Keresse meg őket:

Amint látható, és fuktsii határértéke a függvény az x = 0 egyenlő. Következésképpen, a függvény folytonos az x = 0.

X = 1 Megkeressük a bal oldali korlát ezen a ponton:

Keressen egy jobb oldali korlát:

A határérték funkciója és a függvény értéke a ponton x = 1 kell találni az ágak a funkciót, amely magában foglalja ezt a pontot, azaz a második ága. Keresse meg őket:

Fuktsii limit és a értéke a függvény az x = 1 egyenlő. Következésképpen, a függvény folytonos az x = 1.

X = 3. Keressünk egy bal határ ezen a ponton:

Keressen egy jobb oldali korlát:

A határérték funkciója és a függvény értéke a ponton x = 3, hogy található az ágakat a funkciót, amely magában foglalja ezt a pontot, azaz a második ága. Keresse meg őket:

Fuktsii limit és a értéke a függvény az x = 3 egyenlő. Következésképpen, a függvény folytonos az x = 3.

Így ez a függvény folytonos mindegyik határpont.

Folyamatos változása függvényében lehet meghatározni, mint a fokozatosan változó nélkül ugrik, ahol egy kis változás kis változás együtt jár az érvelés funkciót.

Hadd illusztráljam ezt a folyamatos változást funkció példaként.

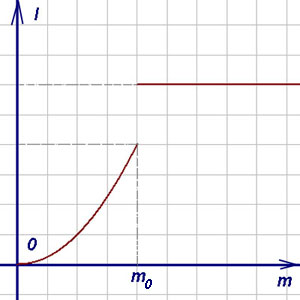
Hagyja a táblázat fölött lóg egy szál terhelést. Hatása alatt ez a terhelés menet van nyújtva, úgyhogy a L távolságra az terhelési felfüggesztési pont fonalat egy a terhelés függvényében m tömegű. azaz L = f (m). m ≥0.

Ha változtatni egy kicsit az áruk tömege, a távolság l keveset változik. Így, kis változások a m ​​megfelelnek az kis változások l. Azonban, ha a terhelés tömege közel van a végső szilárdságát a fonal, egy kis növekedése a rakomány tömegének okozhat szálszakadás: L távolság hirtelen növelése és egyenlővé válik a távolság a felfüggesztés pontjától, hogy az asztal felületét. A grafikon a L = f (m) ábrán mutatjuk be. A telken ez a grafikon folyamatos (szilárd) vonal, és azon a ponton azt felfüggesztették. Az eredmény egy olyan grafikon, amely a két ág. Minden pont, kivéve a függvény L = f (m) folytonos, és van azon a ponton szakadás.

Vizsgálata folytonosságának lehet önálló feladat, és az egyik szakaszában teljes körű vizsgálatot a funkció és építését a menetrend.

A folytonosság a különbség. Legyen a függvény az y = f (x) meghatározott intervallumban] a. b [és folyamatos minden pontján az intervallum. Akkor azt mondta, hogy folytonos a] a. b [. Hasonlóképpen, a koncepció a folyamatosság megállapítása az időközönként formájában] - ∞, b [. ] A. + ∞ [. ] - ∞, + ∞ [. Tegyük fel most, hogy a függvény az y = f (x) meghatározott intervallumon [a. b]. A különbség az intervallumot és az intervallum: intervallum határpont nem szerepelnek az intervallum, és a határ pont az intervallum tartalmazza a szegmens. Itt meg kell említeni az úgynevezett egyoldalú folytonosság: a lényeg a. maradó, az [a. b]. tudjuk megközelíteni csak a jobb és a b pont - csak a bal oldalon. A funkció az úgynevezett folyamatos intervallumban [a. b]. ha ez a folyamatos egyáltalán belső pontja ebben a szegmensben is folyamatos a jobb és bal folyamatos ponton b.

Egy példa a folytonos függvény bármelyik lehet az elemi függvények. Minden egyes elemi függvény folytonos minden intervallumot, amelyben meg van határozva. Például, a funkciók folyamatos és bármikor intervallum [a. b]. folytonos a [0. b]. folytonos bármely intervallum nem tartalmaz az a pont a = 2.

2. példa Annak vizsgálatára funkció folytonosságot.

Határozat. Megnézzük az első feltétel. A funkció nem definiált pontok - a 3. és 3. Legalább az egyik feltétele a folytonosság az egész számegyenesen nem kerül végrehajtásra. Ezért ez a függvény folytonos időközönként

3. példa Annak meghatározására, hogy milyen érték paraméter egész folytonos tartomány funkció

Határozat.
Találunk egy bal limit funkció:

Mi található a jobb oldali határérték, ha:

Nyilvánvaló, hogy az érték azon a ponton, ahol X = 2 legyen egyenlő ax: