folytonos függvények
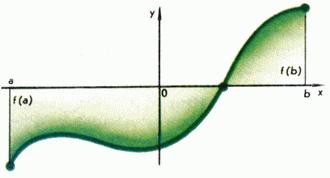
Tekintsük a két funkciót, amelynek grafikonok ábrán mutatjuk be. Az 1. és 2. grafikon az első függvény lehet levonni felemelése nélkül ceruzát a papírról. Ez a funkció az úgynevezett folyamatos. Ütemezése másik funkciót, így lehetetlen, hogy dolgozzon. Két folytonos darab, és van egy rés a ponton, és felhívjuk a repedés funkciót.
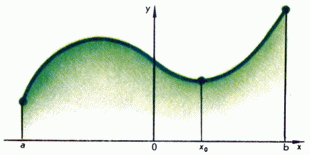
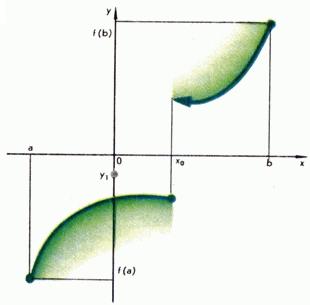
Egy ilyen egyértelmű meghatározása folytonosság nem intézkedik a matematika, mert tartalmaz egy teljesen non-matematikai fogalom „ceruza” és a „papír”. A pontos matematikai definícióját folytonosság adott koncepciója alapján a határ, és a következő.
Hagyja, hogy a függvény az intervallumon és - egy pont ebben a szegmensben. A funkció az úgynevezett folyamatos a ponton, ha a törekvés (látható csak az intervallum) értékek általában működnek, azaz ha
A funkció az úgynevezett folyamatos intervallumon, ha folyamatosan minden pontján.
Ha a pont a (1) egyenlet nem teljesül, a függvény az úgynevezett folytonos a ponton.
Mint látjuk, a folytonosság egy matematikai függvény az intervallum határozza meg a helyi (lokális) folytonosságát a lényeg.
Az érték az úgynevezett növekmény az érvelés, a különbség funkció a növekmény funkció értékek és jelöljük. Nyilvánvaló, hogy az érvvel, hogy a növekmény nullához :.
Nézzük átírni (1) egyenlet az ezzel egyenértékű
Ezzel a jelöléssel lehet átírni:
Tehát, ha a függvény folytonos, akkor az érv nullához növekmény növekmény funkció nullához. Beszélj más módon: egy kis növekmény az érvelés megegyezik kis mértékű növekedése a funkciót. Ábra. A 3. ábra egy grafikon, egy folytonos függvény a ponton, a növekmény megfelel egy növekmény funkciót. Ábra. 4 növekmény megfelel egy változata a funkciót, ami nem számít, hogy milyen kicsi volt, nem lehet kevesebb, mint a fele a szegmens hosszát; függvény folytonos a ponton.
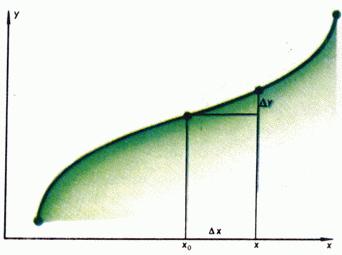
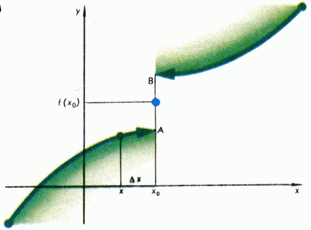
Elképzelésünk folyamatos funkció függvényében, hogy levonhatjuk a grafikonon felemelése nélkül ceruzát a papírról, jól támogatja a tulajdonságait folytonos függvények, amelyek bizonyították a matematikai analízis. Jegyezzük meg, például ilyen tulajdonságokkal rendelkezik.
1. Ha egy folytonos szegmensre a függvény a végén a szegmens értékeit különböző jeleket, majd egy bizonyos ponton ebben az intervallumban tart a nulla értéket.
2. A függvény folytonos az intervallumon, megkap minden közbenső értékek közötti értékeket végén pont, azaz és között.
3. Ha a függvény folytonos intervallumon, akkor ebben az intervallumban nem éri a maximális és a minimális érték, vagyis ha - a legkisebb és - a legnagyobb értéket a függvény az intervallumon, akkor van pont ebben a szegmensben, és hogy.
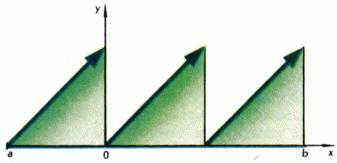
A geometriai jelentése az első ilyen kijelentések elég világos: ha a folytonos görbe halad az egyik oldalról a másik tengely, metszi ezt a tengelyt (5. ábra). Nem folytonos függvény az ingatlan, amint azt a ábra grafikonja. 2, valamint a tulajdonságait a 2. és 3. ábrán. 2, a függvény nem fogadja el az értékét, annak ellenére, hogy fekszik és között. Ábra. A 6. ábra egy példa a folytonos függvény (törtrész), amely eléri a maximális értéket.
Egy példa a folytonos függvény bármelyik lehet az elemi függvények. Minden egyes elemi függvény folytonos minden intervallumot, amelyben meg van határozva. Például, a funkciók folyamatos és bármely intervallumban, az intervallum folyamatos, folytonos függvény bármely intervallumban nem tartalmazó a pontot.
Összeadás, kivonás, szorzás folyamatosan ugyanazon a szegmensben ismét működik vezet folytonos függvények. Ha elosztjuk két folytonos függvények lesz folytonos függvény, ha a nevező értéke nullától eltérő mindenhol.
A koncepció egy folytonos függvény matematikai érkezik, előbb tanulmányozza a különböző törvények a mozgás. Tér és idő folytonos, és a függőség, például az út időről időre kifejezve a törvény által, egy példa egy folytonos függvény.
A folytonos függvények írják állapotok és folyamatok anyagok, folyadékok és gázok. A diákok a tudomány - az elmélet rugalmasságát, hidrodinamikai és aerodinamikai - egyesül egy név - „kontinuum”.