Annak megállapításához, a rácsállandója és az összes főbb csúcsok, fizportal

2. A diffrakciós rács (L) általában beeső monokromatikus fény hullámhossza 0,65 mikron. E. A képernyőn található párhuzamos és attól bizonyos távolságban a rács felett távolságban 0,5 m. A megfigyelt diffrakciós mintázat. A távolság a diffrakciós maximumot elsőrendű egyenlő 10 cm. Határozza meg a konstans a rács és a teljes száma fő csúcsok kapunk ezzel rács.

Határozat.
Írunk a feltétele a fő csúcsok a diffrakciós rács:
dsinφ = kλ (1)
A feltétel az a probléma k = 1. Tekintettel arra, hogy az L / 2 <

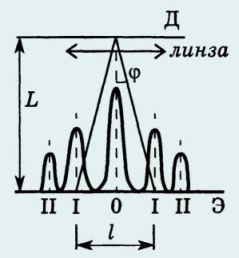
van
sinφ ≈ tgφ = l / (2L). (2)
Behelyettesítve (2) be (1) megkapjuk
dl / (2L) = λ
vagy
d = 2λL / l. (3)
Behelyettesítve a numerikus változók értékeit, azt látjuk,
d = 2 × 6,5 × 10 -7 × 0,5 / 0,1 = 6,5 × 10 -6 = 6,5 (m).
Ahhoz, hogy meghatározzuk a teljes száma fő csúcsok által adott diffrakciós rács, feltételeken alapuló, hogy a maximális eltérítési szög a gerendák a szokásos terjedési iránya nem haladhatja meg a 90 o. t. e. sin90 o = 1. Ekkor az (1) válik
Kmax = d / λ.
Azt, hogy számítások:
Kmax = 6,5 × 10 -6 / (6,5 × 10 -7) = 10.
.. A teljes száma maxima egyenlő n = 2kmax + 1, azaz, jobbra és balra a központi csúcs figyelhető meg maxima Kmax:
n = 2 × 10 + 1 = 21.
Válasz. d = 6,5 mm. Kmax = 10. n = 21.